사인 코사인 탄젠트 표 sin cos tan 쉽게 외우기 삼각비 특수각 뜻
* 출처 : https://blog.naver.com/run_and_run/222843745550
안녕하세요 오늘은 삼각비 뜻과 특수각에 대해서 알아보고 사인 코사인 탄젠트 표(sin cos tan 표)를 설명드리면서 쉽게 외우는 방법까지 자세하게 알려드리도록 하겠습니다. 삼각비 표를 어렵게 외웠던 분들은 제가 알려드리는 내용을 참고하셔서 공부하거나 시험을 볼 때 많은 도움을 받으시면 좋겠네요.
삼각비 뜻
삼각비란 직각삼각형의 세 변의 길이 중 두 변의 길이 간의 비례 관계를 나타내는 값입니다. 보통 각도에 따라서 비율은 변하지만 각이 일정하면 삼각형의 크기와 관계없이 삼각비는 항상 일정해요.
삼각비에서 기본적인 비례 값이 3가지가 있는데 이것이 바로 그 유명한 사인 코사인 탄젠트입니다. 수학 기호는 영어로 sin cos tan 라고 쓰죠. 역수인 코시컨트(csc) 시컨트(sec) 코탄젠트(cot)도 있지만 이건 다음에 다뤄볼게요.
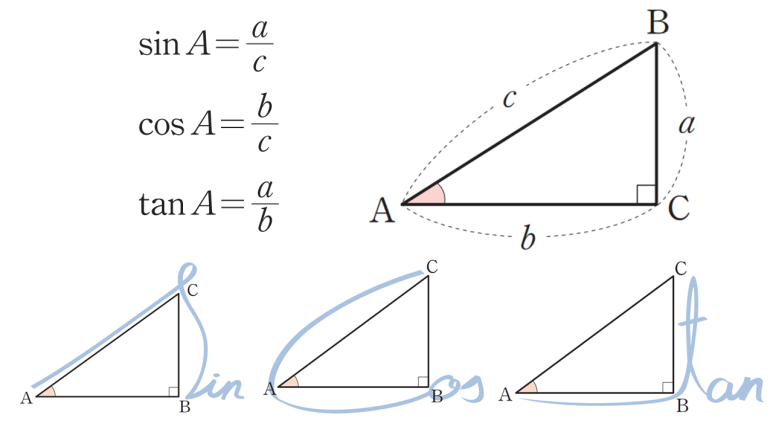
사인 코사인 탄젠트의 정의와 원리를 설명 드릴 텐데요. 위처럼 삼각형을 두고 필기체로 외우는 방식은 나중에 헷갈립니다. 밑변과 높이가 각도의 위치에 따라 달라지기 때문이죠. 그러니 그냥 제가 알려드리는 것으로 이해하세요. 익숙해지면 훨씬 쉽습니다.
직각삼각형은 일단 삼각형이니까 변이 3개, 각이 3개 있습니다. 그리고 각 3개 중 1개가 직각이죠. 삼각형의 내각의 합은 180도이기 때문에 90도가 가장 큰 각이고 나머지 두 각의 크기를 합쳐야 직각이 됩니다.
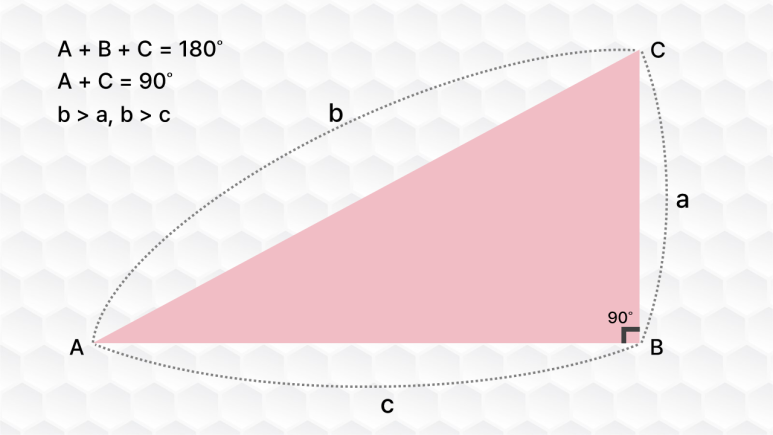
여기까지는 삼각형의 기본적인 성질이니까 쉽게 이해가 되시죠? 이때 빗변은 직각과 마주보는 가장 긴 변이 되기 때문에 직각삼각형이 주어진다면 바로 알아차릴 수 있어요. 하지만 밑변과 높이는 다른 각도가 주어져야 알 수 있죠. 그래서 그런건 아니지만 빗변을 삼각비에서 기준이 된다고 생각하시면 좋아요.
사인 뜻
사인(sine)은 직각삼각형의 빗변과 높이의 비(높이/빗변)입니다. 아까 빗변이 기준이라고 했으니 쉽게 외우려면 그냥 '높이'로 기억하셔도 됩니다. 기준은 항상 분모로 쓰면 되니까요. 기호를 쓰면 sin이 되고 sin30˚, sin60˚, sin90˚ 이런식으로 씁니다.
코사인 뜻
코사인(cosine)은 직각삼각형의 빗변과 밑변의 비(밑변/빗변)입니다. 역시 쉽게 외우려면 그냥 '밑변'으로 기억하셔도 됩니다. 기호는 cos이고 cos30˚, cos60˚, cos90˚ 이런식으로 씁니다.
코사인의 기원을 보면 사인에 co-라는 접두사를 붙인 것은 사인을 보충한다는 뜻을 나타냅니다. 쉽게 말해서 90도를 기준으로 사인에서 부족한만큼 보충하는 것이 코사인이고, 이러면 외우지 않고도 아래와 같은 성질을 저절로 알게 됩니다. (우리나라 말로는 여각이라고도 해요.)
$\sin x\ =\ \cos \left(90\cir -x\right)$sinx = cos(90°−x)
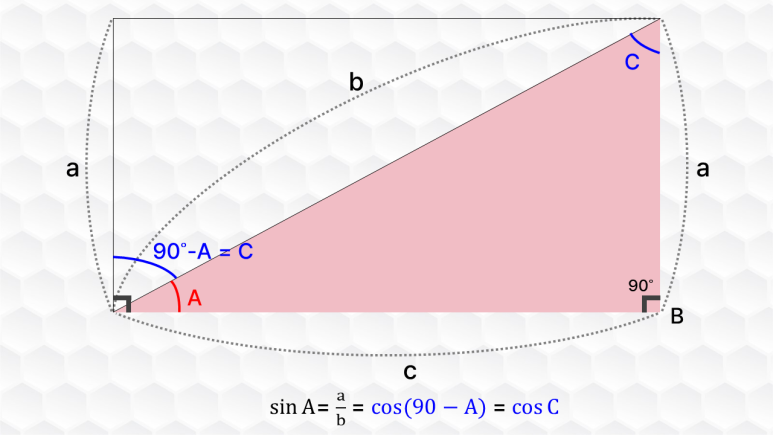
탄젠트 뜻
앞에 내용을 보다보면 탄젠트(tangent)는 기준이 다른데?라고 생각하실 수 있는데요. 사실, 탄젠트는 사인 코사인의 비율(사인/코사인)입니다. 각각 분모가 같아서 약분하면 높이/밑변이 되는 것이죠. tangent의 영어 뜻은 접선이란 뜻입니다. 빗변을 기준으로 원을 그렸을 때, 그 접선과 만나는 밑변의 연장선의 길이가 탄젠트가 되기 때문입니다. 역시 기호는 tan입니다.
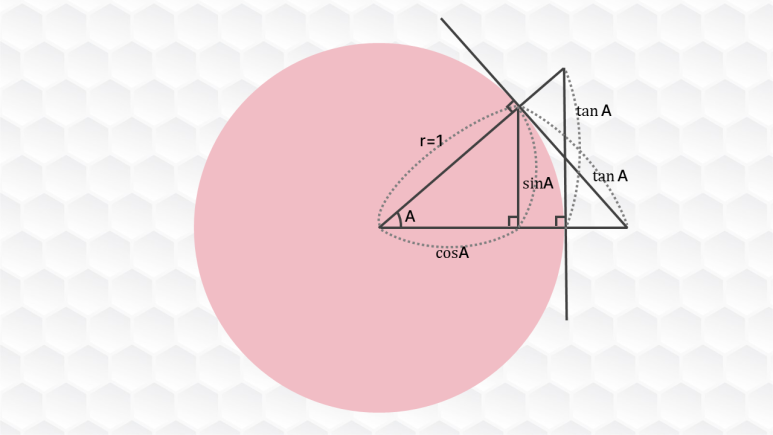
삼각함수를 설명하면 위 내용에 대해서 더 자세하게 말씀드릴 수 있겠지만 오늘은 삼각비의 표에 대해서 알려드리기로 했으니 여기까지만 다루도록 할게요.
삼각비 특수각 뜻
삼각비 특수각은 0도, 30도, 45도, 60도, 90도입니다. 일반적인 다른 각과는 달리 값이 딱 맞게 떨어지기 때문에 그만큼 실생활에서도 중요하고 삼각비의 활용 문제에도 많이 나오는 각입니다.
특수각에서 삼각비 값은 피타고라스 공식만 알아도 쉽게 구할 수 있어요. 그래서 중2때 피타고라스 정리를 배우면 바로 중3 삼각비를 배우게 되죠. 먼저 특수각인 0˚, 30˚, 45˚, 60˚, 90˚의 삼각비 값을 하나씩 구하고 나서 삼각비 특수각 표를 한눈에 볼 수 있게 정리해볼게요.
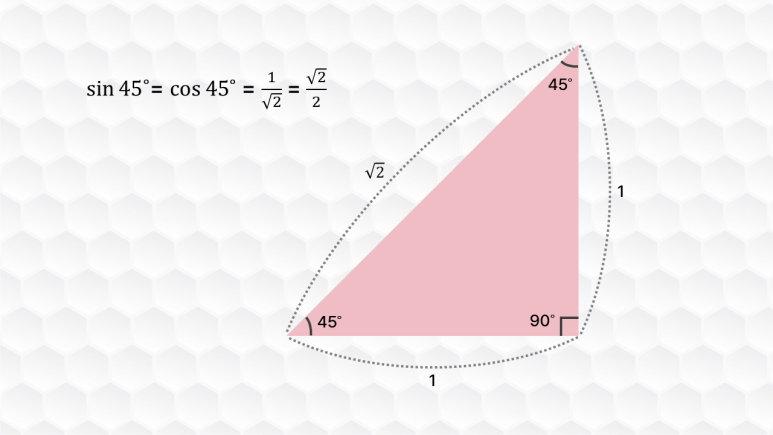
45도는 위 그림처럼 직각이등변삼각형을 보면 됩니다. 양변의 길이가 1일 때 피타고라스 정리에 의해서 빗변의 길이는 루트2 가 돼죠. 이때는 sin45˚와 cos45˚는 아래처럼 똑같습니다.
$\sin 45\cir \ =\ \cos 45\cir \ =\ \frac{1}{\sqrt{2}}\ =\ \frac{\sqrt{2}}{2}$sin45° = cos45° = 1√2 = √22
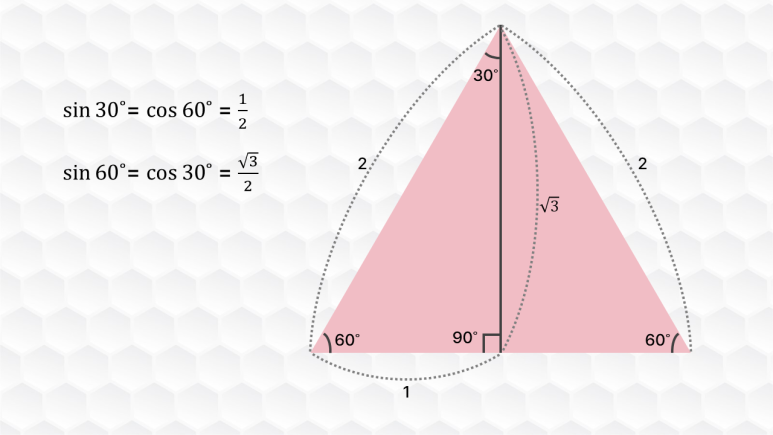
30도와 60도일 때는 위처럼 정삼각형을 생각하세요. 빗변 길이가 2면 밑변은 1, 높이는 루트3이 돼요. sin30˚는 1/2이고 이것은 cos60˚와 같아요. sin60˚는 루트3/2가 되고 이는 cos30˚와 같죠.
$\sin 30\cir \ =\ \cos 60˚\ =\ \frac{1}{2}$sin30° = cos60˚ = 12
$\sin 60˚\ =\ \cos 30˚\ =\frac{\sqrt{3}}{2}$sin60˚ = cos30˚ =√32
마지막으로 0도와 90도는 사실 삼각형으로 그릴 수가 없기 때문에 그냥 직선을 생각합니다. 0도는 빗변과 밑변이 같은 직선이 되겠죠. 그럼 높이는 0이고 sin0은 0, 밑변과 빗변은 같아져서 cos0은 1이 됩니다. 90도는 빗변과 높이가 같은 직선을 생각해봐요. 반대로 sin90은 1, cos90은 0이 됩니다.
탄젠트는 사인에서 코사인을 나누면 된다고 했죠? tan0은 0÷1이라 0, tan30은 1/2÷ √3/2여서 1/√3, 분모 유리화하면 √3/3입니다. tan45는 1, tan60은 tan30의 역수니까 √3, tan90은 0으로 나눌 수 없으니 값이 없습니다.
사인 코사인 탄젠트 표와 암기법
지금까지 계산한 것을 정리하면 아래처럼 sin cos tan 표로 나타낼 수 있습니다.
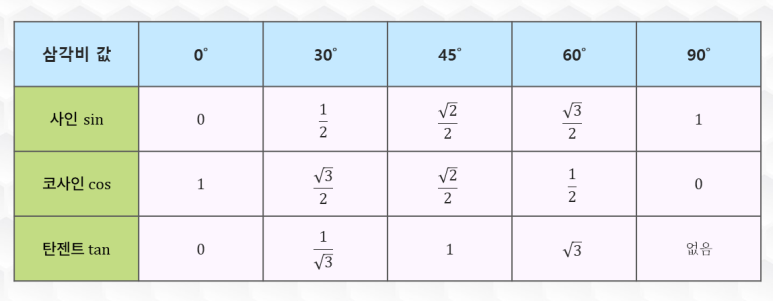
앞서 코사인이 90도에서 부족한 각도의 사인과 같다고 했는데요. 표를 보면 다시 한 번 확인이 됩니다. 사인만 외워도 코사인은 저절로 암기가 되는 것이죠. 사인 암기법도 매우 쉽습니다. 0도, 30도, 45도, 60도, 90도가 순서대로 루트0, 루트1, 루트2, 루트3, 루트4에서 2를 나눈 값이니까요.
탄젠트는 사인/코사인이니까 따로 암기할 필요가 전혀 없습니다. 이렇게 하면 사인 값 하나로 코사인과 탄젠트까지 한 번에 외워지죠?
사인 코사인 탄젠트 표를 삼각비 특수각만으로 나타내는 것이 아니라 0부터 180까지 1˚ 단위로 상세한 수치를 알고 싶다면 아래 이미지를 확인하세요. 왼쪽부터 사인 표, 코사인 표, 탄젠트 표 순서대로 보면 됩니다.
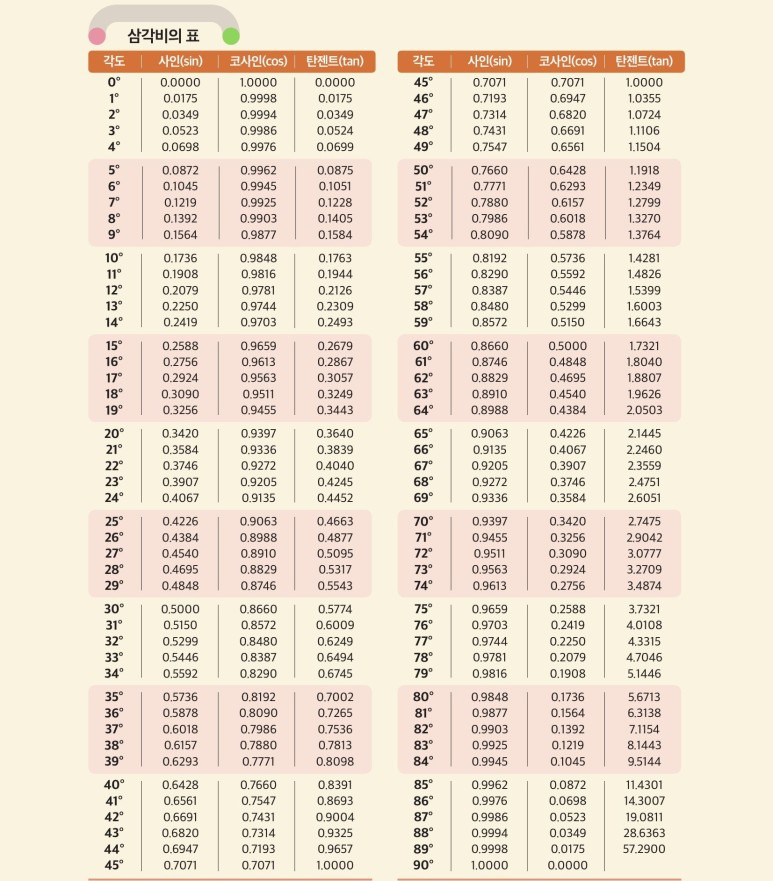
출처 : 미래엔 중3 수학 교과서
우리나라 수학 교육과정에서 중학교 3학년 2학기때 삼각비를 배우는데요. 고등학교에서 이 개념을 활용해서 삼각함수와 그 미적분, 기하벡터 등을 공부하게 됩니다. 제가 고등학교 때 이 부분의 기초가 부족해서 상당히 고생했던 기억이 있는데요. 제가 쓴 내용을 보고 sin cos tan 표 쉽게 외우기에 성공하시고 학습에 도움이 되시길 바랍니다. 읽어주셔서 진심으로 감사합니다.


요점정리 너무 감사합니다..ㅜ
답글삭제